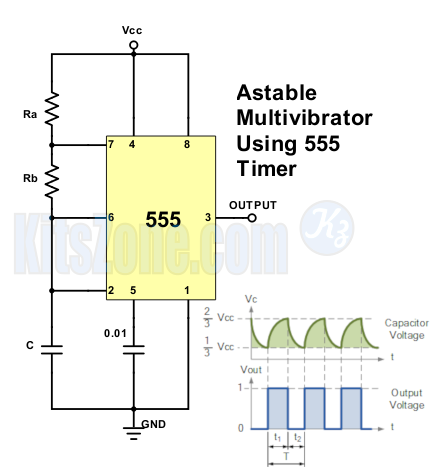
The IC 555 timer is connected for astable operation. Only one resistor is used as timing resistor in monostable multivibrator using 555 and here the timing resistor is split into two sections as Ra and Rb, with the discharge pin (pin 7) is connected to the junction of Ra and Rb.
The astable multivibrator circuit utilizing the versatile 555 timer IC is a remarkable innovation in electronic circuitry. With its distinctive oscillating characteristic, the astable multivibrator serves as a fundamental building block for many electronic devices. The ingenious arrangement of resistors and capacitors within this circuit generates a continuous and unique waveform, allowing for a wide range of applications in fields such as telecommunications, timing devices, and frequency generation. The astable multivibrator's ability to produce a continuous square waveform with no stable state makes it an invaluable tool for various electronic projects, ensuring its place as a staple component in countless innovative designs.
The capacitor is charged and discharged periodically between 1/3 of Vcc and 2/3 of Vcc.
The output stage is High during the charging cycle for a time period t1, so
$$t_{1}=(R_{a}+R_{b})C \text{ } ln{\frac{V_{cc}-\frac{1}{3}V_{cc}}{V_{cc}-\frac{2}{3}V_{cc}}}$$
$$t_{1}=(R_{a}+R_{b})C \text{ } ln{\frac{3V_{cc}-V_{cc}}{3V_{cc}-{2}V_{cc}}}$$
$$t_{1}=(R_{a}+R_{b})C \text{ } ln{\frac{2V_{cc}}{V_{cc}}}$$
$$t_{1}=(R_{a}+R_{b})C \text{ } ln{2}$$
$$\therefore t_{1}=0.693(R_{a}+R_{b})C ---- (1)$$
The output stage is low during the discharge cycle for a time period t2
$$\therefore t_{2}=0.693(R_{b})C ---- (2)$$
So, the total time period for charging and discharging is,
$$T=t_{1}+t_{2}$$
$$T=0.693(R_{a}+2R_{b})C$$
Output frequency is given as,
$$f=\frac{1}{T}=\frac{1.443}{(R_{a}+2R_{b})C}$$
DUTY CYCLE
The duty cycle D of a recurring output is defined as the ratio of the High time to the total cycle,
$$D=\frac{t_{1}}{T}=\frac{R_{a}+R_{b}}{R_{a}+2R_{b}}$$